RPMTurbo
Specialists in Linear Flow Analysis

2D Steam Turbine Flutter Test Case

RPMTurbo has developed a 2D steam turbine flutter test case. The geometry and flow conditions are similar to those of a typical industrial steam turbine near the tip. The tip region is critical for flutter analysis because this is where most of the unsteady aerodynamic work that drives flutter occurs. The test case has the following features that differ from other standard 2D flutter test cases:

  • high stagger angle
  • high Mach number
  • non-uniform steady flow at outlet.

    • Problem Description

    The geometry is a 2D cascade of flat plates with half circles at the leading and trailing edge and a high stagger angle (78 degrees). The isentropic Mach number at the turbine exit is high (1.362). A complete description of the geometry and the flow conditions for the test case are given in the tables below.

    Geometry
    Profile flat plate
    Chord length 222.5 mm
    Stagger angle 78.0 deg
    Thickness 2.5 mm
    Pitch gap 198 mm
    LE and TE half circles
    Flow Conditions
    Inlet pressure 24 kPa
    Total temperature 340 K
    Inflow angle 78 deg
    Incoming Turbulence 4.52%
    Exit pressure 9 kPa

    The flow is assumed to be viscous and the ideal steam properties chosen for this test case are shown in the table below. The aim of the test case is to calculate the flutter stability (aerodynamic damping) due to a blade vibrational mode with motion normal to the blade (similar to a 3D bending mode). The description of the vibrational mode is given in the table below.

    Ideal Steam Properties
    Ratio of specific heats 1.11
    Gas Constant 461.52 J/kg.K
    Absolute viscosity 1.1e-5 Pa.s
    Blade Mode
    Mode Shape rigid-body translation
    Direction normal to chord
    Frequency 100 Hz

    Mesh

    RPMTurbo has created three multi-block meshes for this test case. The long and short domains have the inlet and outlet planes at different locations. The details of the meshes are shown in the table below. Each mesh has an O mesh around the profile. The long domain mesh is shown in the figures below. There are links to download the meshes in the table below. The meshes are stored in cgns files as unstructured meshes of hexahedral cells.
    Mesh Long Domian Short Domain Fine Mesh
    Number of cells 10285 9829 39932
    Min mesh angle (degrees) 42.24 39.86 37.83
    Average height of first cell on profile (m) 1.76e-5 1.74e-5 1.2e-5
    Centre of half circle at leading edge (m) (0.0, 0.0) (0.0, 0.0) (0.0, 0.0)
    Centre of half circle at trailing edge (m) (0.045741, 0.215192) (0.045741, 0.215192) (0.045741, 0.215192)
    Axial location of inlet (m) -0.100 -0.0500 -0.100
    Axial location of outlet (m) 0.1457 0.1000 0.1457
    CGNS file longDomain.cgns (1.79 Mb) shortDomain.cgns (1.71 Mb)

    Steady-State Solutions

    Steady-state solutions for this test case were calculated by RPMTurbo's LUFT code. The flow model was the Reynolds-averaged Navier-Stokes equations with the Spalart and Allmaras Turbulence model. The flow was assumed to be fully turbulent with the incoming Spalart and Allmaras turbulence variable set to 0.1. This corresponds to an incoming turbulent intensity equal to 4.52%. Details of the steady-state solution calculated on the long domain are shown in the table below.

    Inlet Mach Number 0.699
    Outlet Mach number 1.312
    Reynolds number (based on outlet conditions) 664 183
    Average y+ on profile 1.20

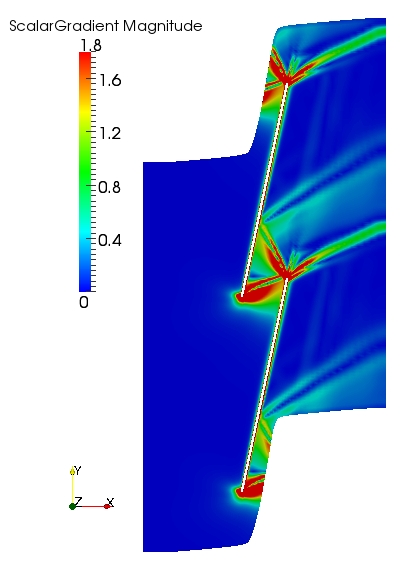
    The steady-state Mach number of the flow-field calculated on the long and short domain meshes are shown below (left). The flow-fields are similar for both domains and the steady-state solution is independent of the far-field location. Also, there is no evidence of reflections of the steady waves at the inlet and outlet of the domain from the numerical schlieren plot (magnitude of density gradient) shown below (right).

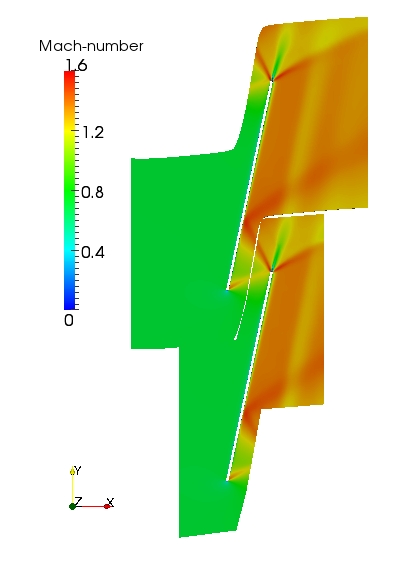
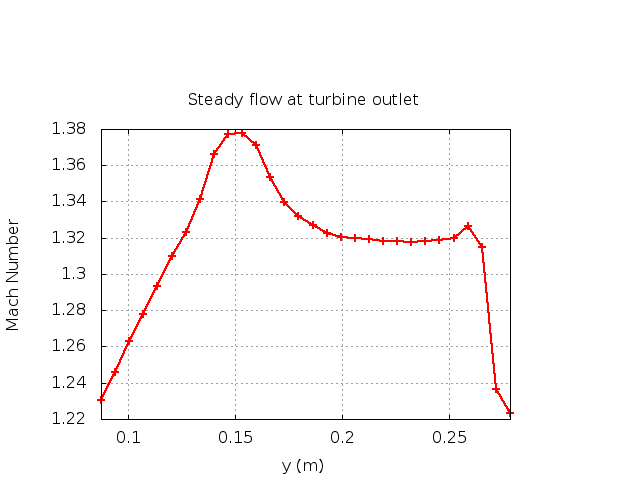
    One characteristic of this test case is that the steady flow at the outlet is not uniform. The variation in the Mach number in the pitch-wise direction can be seen in the plot below.

    Unsteady Flow Solutions

    The flutter analysis is performed by calculating the unsteady flow response due to the blade vibrating at the prescribed mode shape at various interblade phase angles (IBPA). The IBPA is the constant difference in the phase angle of the blade motion between adjacent blades. It is necessary to calculate the unsteady flow response at all possible interblade phase angles, in order to consider the effects of the aerodynamic and structure coupling between the blades. The aerodynamic damping is the non-dimensional damping work done by the aerodynamics on the blade motion. If the aerodynamic damping is negative, then there is a potential flutter problem.

    The aerodynamic damping calculated by the RPMTurbo LUFT code for this test case is shown below. RPMTurbo's 3D non-reflecting boundary condition (3D-NRBC) was applied at the inlet and outlet. The solutions were calculated on the short, long and fine meshes. The aerodynamic damping calculated on the three meshes agree well. This demonstrates that the solutions are independent of the mesh resolution and location of the inlet and the outlet.